그래프(Graphs)

A graph data structure consists if a finite (and possibly mutable) set of vertices or nodes or points, together with a set of unordered pairs of there vertices for an undirected graph or a set of ordered pairs for a directed graph. 

• 노드와 노드가 연결된 비선형 자료 구조이다.
• Vertex (= a node) / Edge (= conntection between nodes)로 이루어져 있다.
• 트리도 그래프의 일종이다.

ex) social network, location, mapping, routing argorithms etc...

 

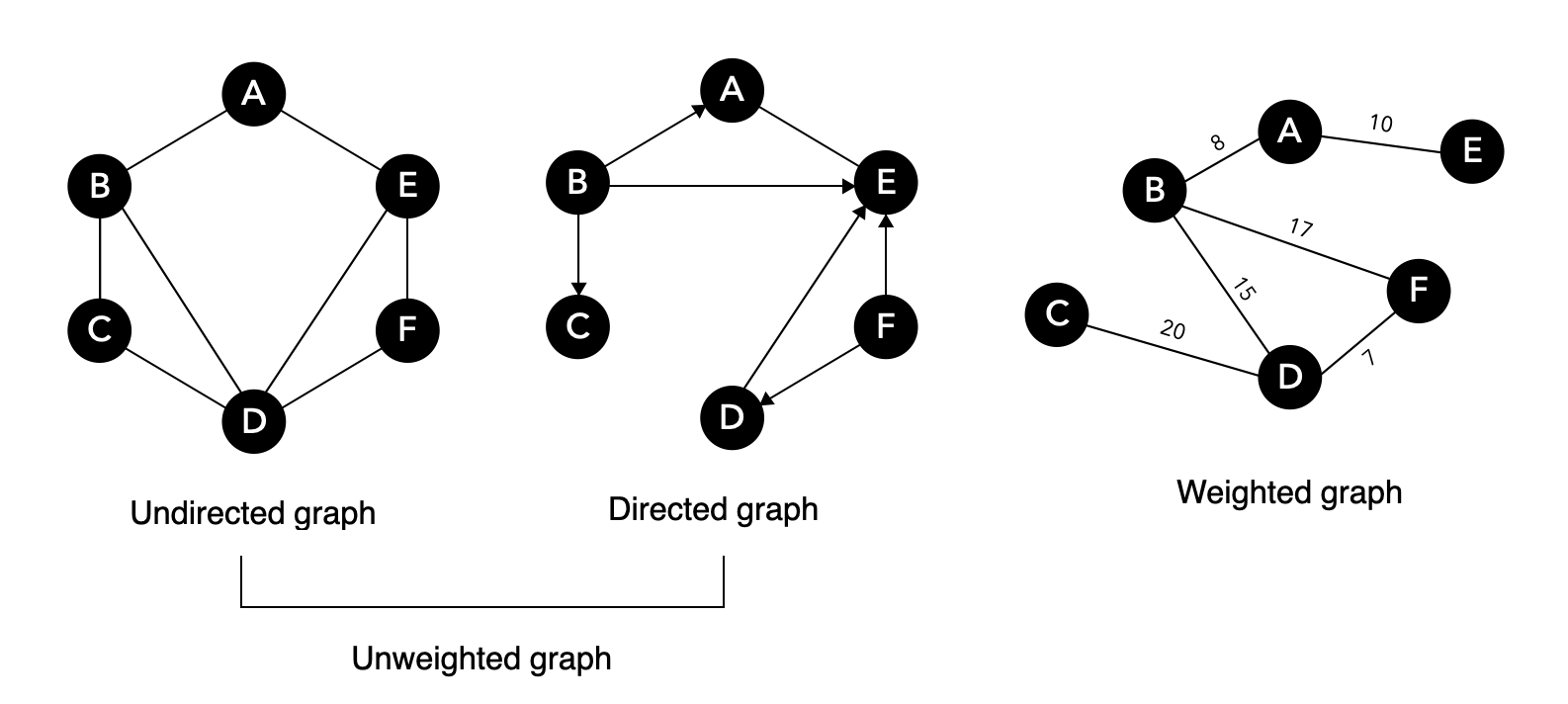
그래프의 구현 방법

인접 행렬	인접 리스트
vertex의 제곱만큼 공간을 차지 (퍼져있는 데이터 기준)	더 적은 공간을 차지 (퍼져있는 데이터 기준)
모든 간선(edges)를 순회하는데 느리다	모든 간선(edges)를 순회하는데 빠르다
특정 간선(edge)을 찾는데 빠르다	특정 간선(edge)을 찾는데 느리다

→ 실제 세상에서 사용되는 데이터의 연결은 생각보다 많지 않다. 때문에 적은 공간을 차지하는 인접 리스트 방법이 더 매력적이다!

 

 

인접 리스트(무방향 그래프) 구현

class Graph{
    constructor(){
        this.adjacencyList = {}; // 객체로 설정
    }
    addVertex(vertex){
    	// 해당하는 vertex가 없다면, 해당 키에 빈 배열을 만든다
        if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
    }
    addEdge(v1,v2){
    	// vertex1의 키를 찾아서 vertex2를 넣는다
        this.adjacencyList[v1].push(v2);
        // vertex2의 키를 찾아서 vertex1를 넣는다
        this.adjacencyList[v2].push(v1);
    }
   removeEdge(vertex1,vertex2){
   	// vertex1에서 제거하고자 하는 vertex2가 아닌 요소들로 새로운 배열 반환
        this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
            v => v !== vertex2
        );
        // vertex2에서 제거하고자 하는 vertex1이 아닌 요소들로 새로운 배열 반환
        this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
            v => v !== vertex1
        );
    }
    removeVertex(vertex){
    	// 제거해야 할 vertex를 확인하기 위해서는 모든 루프를 순회하여야 한다
        while(this.adjacencyList[vertex].length){
        	// 특정 vertex 키에 접근하여 값을 제거하면 removeEdge가 호출된다
            const adjacentVertex = this.adjacencyList[vertex].pop();
            // 제거 대상 vertex와 연결된 vertex를 전달하여 연결을 끊어준다
            this.removeEdge(vertex, adjacentVertex);
        }
        // 해당 vertex의 키를 삭제한다 (빈 배열로 키가 남아있기 때문에)
        delete this.adjacencyList[vertex]
    }
}

let g = new Graph();
g.addVertex("Dallas");
g.addVertex("Tokyo");
g.addVertex("Aspen");
g.addVertex("Los Angeles");
g.addVertex("Hong Kong")
g.addEdge("Dallas", "Tokyo");
g.addEdge("Dallas", "Aspen");
g.addEdge("Hong Kong", "Tokyo");
g.addEdge("Hong Kong", "Dallas");
g.addEdge("Los Angeles", "Hong Kong");
g.addEdge("Los Angeles", "Aspen");